PITÁGORAS Y SU TEOREMA

Comenzamos esta nuestra última semana de matemáticas hablando de triángulos, para lo que en primer lugar hemos definido algunos términos.

Un triángulo es una figura geométrica que consta de tres lados que, a su vez, forman tres ángulos y que, además, tienen tres vértices. La suma de los ángulos internos de un triángulo (da igual cuál sea) siempre es de 180º.

En función de cómo tenga los lados y los ángulos, podemos clasificarlos en tres tipos:

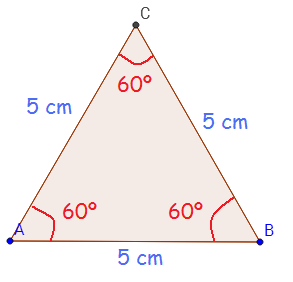
• Equiláteros: tienen los tres lados y los tres ángulos iguales.
  
• Isósceles: tienen dos lados iguales y, los dos ángulos que forman esos lados con el lado desigual, también iguales.
  
• Escalenos: tanto los tres lados como los tres ángulos son diferentes.
  

Además, también podemos clasificar a los triángulos por los tipos de ángulos que presentes de la siguiente manera:

• Obtusángulos: tienen un ángulo de más de 90º (ángulo obtuso, de ahí su nombre).
  
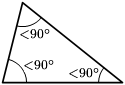
• Acutángulos: todos sus ángulos miden menos de 90º (ángulos agudos, de ahí el nombre de nuevo).
  
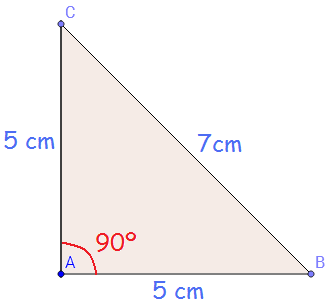
• Rectángulos: tienen un ángulo de 90º (ángulo recto).
  

Y justamente estos últimos son los que nos interesan para el llamado Teoréma de Pitágoras, ya que únicamente en ellos es en los que lo podremos utilizar. Y para ello es necesario ponerle nombre a los diferentes lados de este tipo de triángulos.

Al lado que encontramos enfrente del ángulo recto, el más largo de los tres, le denominamos hipotenusa, mientras que cada uno de los que forman dicho ángulo recibe el nombre de cateto, de tal manera que todo triángulo rectángulo tiene una hipotenusa y dos catetos.

Llegados a este punto solo nos queda explicar el Teorema de Pitágoras, que nos dice que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, es decir, que si hacemos un cuadrado a partir de cada lado del triángulo (uno a partir de la hipotenusa y otro a partir de cada cateto) y sumamos lo que ocupan los dos de los catetos, el resultado es igual a lo que ocupa el de la hipotenusa.

Matemáticamente lo escribimos así:

hipotenusa² = cateto 1² + cateto 2²

h² = c1² + c2²

Esto nos sirve para, cuando conocemos dos lados de un triángulo rectángulo, poder calcular el que falta, lo cual tiene muchísimas aplicaciones en geometría, física y hasta química, pero que "por desgracia" no vamos a ver en este curso. Así, os tendréis que fiar de mi palabra y creeros lo que os digo, pero veamos algún ejemplo numérico.

En un primer caso, imaginémonos que conocemos los dos catetos pero desconocemos la hipotenusa. Dichos catetos miden 3 y 4 cm, por ejemplo. Para saberlo solo tenemos que sustituir en la fórmula matemática del teorema los valores que conozcamos donde corresponda:

h² = c1² + c2²

Como c1 es 3 y c2 es 4 (podríamos haberlos nombrado al revés y daría igual):

h² = 3² + 4²

Hacemos los cuadrados:

h² = 9 + 16

Hacemos la suma:

h² = 25

Por último, quitamos el cuadrado de la hipotenusa haciendo la raíz cuadrada del número que nos queda:

h = √25

h = 5

Ya sabemos que cuando un cateto vale 3 cm y el otro 4 cm la hipotenusa vale 5 cm.

También se puede dar el caso de que conozcamos la hipotenusa y un cateto, por ejemplo 15 cm y 9 cm, respectivamente. En este caso operaremos así:

h² = c1² + c2²

Como h es 15 y c1 es 9 (también podría ser c2, da igual):

15² = 9² + c2²

Pasamos el cateto al cuadrado al otro lado de la igualdad con las reglas de las ecuaciones, es decir, cambiándole el signo:

15² - 9² = c2²

Hacemos los cuadrados:

225 - 81 = c2²

Realizamos la resta:

144 = c2²

Al igual que en el caso anterior, para quitar el cuadrado, hacemos la raíz del número:

√144 = c2

12 = c2

Es decir, que el cateto que nos falta mide 12 cm.

Con esto acabamos lo referente al Teorema de Pitágoras y pasamos, mañana, a las figuras geométricas, longitudes y áreas, lo último que vamos a ver en el curso.