ULTIMANDO CONTENIDOS Y RECORDANDO CONCEPTOS

            Dicen que nada es eterno. Este curso ha tenido un comienzo, como es lógico, y ahora va a tener un final. Ya estamos llegando a la cima de este gran recorrido que habéis hecho todas vosotras y que, como podéis ver, ni se ha hecho tan pesado ni ha sido tan difícil llevarlo a cabo; aunque hay para todos los gustos: a unas les habrá gustado más que a otras, o habrá podido resultar más o menos interesante, o simplemente habrá podido parecer un rollazo. Pero, sea como sea ahí está el resultado.

            En clase, a veces, hemos hecho alusión a lo que supone hacer algo como lo que os ha tenido entretenidas y, en ocasiones, pesadumbrosas: COMPETENCIAS CLAVE. No solo es hacer un curso para obtener un certificado, pues los momentos vividos quedan para siempre, y de todo se aprende. Ya sabéis que el aprendizaje que llevamos a cabo es ese de día a día: aprender unos contenidos, saber cómo piensan los demás, saber que no solo son los niños o adolescentes los que estudian, etc.

            Solo nos quedan dos días en los que dedicaremos el tiempo a recordar, de manera más madurada, todo o casi todo lo visto, para que quede más claro. Espero que todo os sea leve y que os queden ganas para seguir aprendiendo muchas más cosas.


            Mañana nos vemos de nuevo... ah y llevaré mi nuevo collar!!!!  Gracias chicas por todo.




         

PITÁGORAS Y SU TEOREMA

Comenzamos esta nuestra última semana de matemáticas hablando de triángulos, para lo que en primer lugar hemos definido algunos términos.

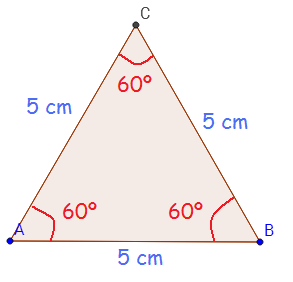
Un triángulo es una figura geométrica que consta de tres lados que, a su vez, forman tres ángulos y que, además, tienen tres vértices. La suma de los ángulos internos de un triángulo (da igual cuál sea) siempre es de 180º.

En función de cómo tenga los lados y los ángulos, podemos clasificarlos en tres tipos:

• Equiláteros: tienen los tres lados y los tres ángulos iguales.
  
• Isósceles: tienen dos lados iguales y, los dos ángulos que forman esos lados con el lado desigual, también iguales.
  
• Escalenos: tanto los tres lados como los tres ángulos son diferentes.
  

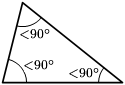
Además, también podemos clasificar a los triángulos por los tipos de ángulos que presentes de la siguiente manera:

• Obtusángulos: tienen un ángulo de más de 90º (ángulo obtuso, de ahí su nombre).
  
• Acutángulos: todos sus ángulos miden menos de 90º (ángulos agudos, de ahí el nombre de nuevo).
  
• Rectángulos: tienen un ángulo de 90º (ángulo recto).
  

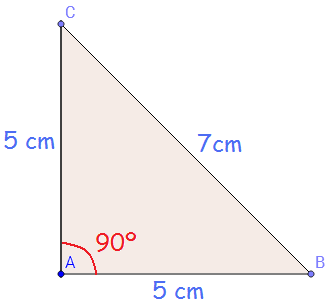
Y justamente estos últimos son los que nos interesan para el llamado Teoréma de Pitágoras, ya que únicamente en ellos es en los que lo podremos utilizar. Y para ello es necesario ponerle nombre a los diferentes lados de este tipo de triángulos.

Al lado que encontramos enfrente del ángulo recto, el más largo de los tres, le denominamos hipotenusa, mientras que cada uno de los que forman dicho ángulo recibe el nombre de cateto, de tal manera que todo triángulo rectángulo tiene una hipotenusa y dos catetos.

Llegados a este punto solo nos queda explicar el Teorema de Pitágoras, que nos dice que en un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa, es decir, que si hacemos un cuadrado a partir de cada lado del triángulo (uno a partir de la hipotenusa y otro a partir de cada cateto) y sumamos lo que ocupan los dos de los catetos, el resultado es igual a lo que ocupa el de la hipotenusa.

Matemáticamente lo escribimos así:

hipotenusa² = cateto 1² + cateto 2²

h² = c1² + c2²

Esto nos sirve para, cuando conocemos dos lados de un triángulo rectángulo, poder calcular el que falta, lo cual tiene muchísimas aplicaciones en geometría, física y hasta química, pero que "por desgracia" no vamos a ver en este curso. Así, os tendréis que fiar de mi palabra y creeros lo que os digo, pero veamos algún ejemplo numérico.

En un primer caso, imaginémonos que conocemos los dos catetos pero desconocemos la hipotenusa. Dichos catetos miden 3 y 4 cm, por ejemplo. Para saberlo solo tenemos que sustituir en la fórmula matemática del teorema los valores que conozcamos donde corresponda:

h² = c1² + c2²

Como c1 es 3 y c2 es 4 (podríamos haberlos nombrado al revés y daría igual):

h² = 3² + 4²

Hacemos los cuadrados:

h² = 9 + 16

Hacemos la suma:

h² = 25

Por último, quitamos el cuadrado de la hipotenusa haciendo la raíz cuadrada del número que nos queda:

h = √25

h = 5

Ya sabemos que cuando un cateto vale 3 cm y el otro 4 cm la hipotenusa vale 5 cm.

También se puede dar el caso de que conozcamos la hipotenusa y un cateto, por ejemplo 15 cm y 9 cm, respectivamente. En este caso operaremos así:

h² = c1² + c2²

Como h es 15 y c1 es 9 (también podría ser c2, da igual):

15² = 9² + c2²

Pasamos el cateto al cuadrado al otro lado de la igualdad con las reglas de las ecuaciones, es decir, cambiándole el signo:

15² - 9² = c2²

Hacemos los cuadrados:

225 - 81 = c2²

Realizamos la resta:

144 = c2²

Al igual que en el caso anterior, para quitar el cuadrado, hacemos la raíz del número:

√144 = c2

12 = c2

Es decir, que el cateto que nos falta mide 12 cm.

Con esto acabamos lo referente al Teorema de Pitágoras y pasamos, mañana, a las figuras geométricas, longitudes y áreas, lo último que vamos a ver en el curso.

CUMPLEAÑOS VARIOS

El curso ya está acabando, el buen tiempo está aquí y se va notando la alegría en el ambiente.

Hoy habéis celebrado el cumpleaños múltiple de Simo, Araceli y Patri: queso, tortilla, tartas,... ¡todo buenísimo!

Para que quede constancia, aquí tenéis fotos de grupo que habéis hecho vosotras mismas.

¡Felicidades, chicas!

ECUACIONES DE PRIMER GRADO

Esta semana no he actualizado mucho porque me reservaba para el último día. Ahora que ya hemos visto todo lo que voy a explicar sobre las ecuaciones os lo dejo aquí plasmado y, así, no os hago tanto lío.

Recordad que existen ecuaciones muy complicadas, diferentes y con una o varias incógnitas, pero aquí nos vamos a centrar solo en las de primer grado sin denominadores (las más sencillitas, podríamos decir).

Para empezar os pongo algunas normas sueltas y, ya al final, los pasos que seguiremos para resolver una ecuación. Vamos a ello.

 

Una ecuación es una igualdad, es decir, una expresión matemática en la que tenemos operaciones o números a ambos lados del signo matemático de igual. Un ejemplo de igualdad sería la siguiente:

3 + 4 = 7

Como lo que hay a ambos lados del signo de igual vale lo mismo, decimos que es una igualdad.

La peculiaridad de las ecuaciones es que son igualdades en las que desconocemos, al menos, alguno de los números, que sustituimos por letras. Por ejemplo, si me dicen que la altura de un árbol es el doble que la de un arbusto de 1,5 metros, yo puedo llamar a la altura del árbol por una letra, y decir que es igual a 1,5 por 2: 

x (altura del árbol) = 1,5 · 2.

Podemos utilizar cualquier letra que se nos ocurra pero, por norma general y convenio, utilizaremos la x, a la que llamamos incógnita de la ecuación.

Los números sueltos que haya en la ecuación no representan ninguna incógnita y podremos operar con ellos siguiendo unas reglas. A cada uno de estos números lo llamamos término independiente.

Además una ecuación se divide en dos miembros: el primero (que incluye todos los términos e incógnitas al lado izquierdo del signo de igualdad) y el segundo (que incluye a los de la derecha).

En una ecuación lo que queremos es averiguar el valor de la incógnita, para lo que tenemos que "despejarla", lo que quiere decir que tenemos que ir simplificándola hasta que nos quede una expresión del tipo x = 9, donde el 9 lo he puesto como ejemplo, pero puede ser cualquier número, positivo a o negativo, y sería la solución de la ecuación.

Un número delante de una incógnita (letra) nos indica el número de veces que tenemos esa incógnita. Matemáticamente lo que hace ese número es multiplicar a la incógnita, como en otras operaciones con números de la vida real: si tengo 4 sacos de patatas y cada saco cuesta 2 euros, el 4 multiplica al 2 para calcular el total (4·2 o 2+2+2+2). Si yo no supiese el precio y le llamase "x", sería lo mismo, 4 sacos por "x" (4x = 4·x = x+x+x+x). A estos números delante de incógnitas se les denomina coeficientes.

 

Vamos a ver ahora los pasos que hay que seguir para resolver una ecuación con una como ejemplo en la que iremos realizando los pasos.

Ejemplo:       6x - 8 = 3x + 4 - x

1º Pasamos a un miembro (lado) todos los números sueltos (términos independientes) y al otro todos los que tengan "x" (incógnitas). Los que no cambian de lado mantiene su signo. Los que cambian, cambian de signo.

Ejemplo:       6x - 8 = 3x + 4 - x

                     6x - 3x + x = 4 + 8

En este caso hemos decidido poner todos los términos independientes a la derecha y las incógnitas a la izquierda, de tal forma que nos quedan en el primer miembro el 6x (mantiene su signo por no cambiar de lado), el 3x (pasa a -3x por cambiar de lado) y el -x (también cambia de signo a +x por cambiar de lado) y en el segundo el 4 (no cambia de lado ni de signo) y el -8 (pasa a +8 al cambiar de lado).

2º Hacemos las operaciones de cada miembro.

Ejemplo:        4x = 12

En el miembro de la izquierda nos queda 4x, ya que teníamos 6 (6x) le restamos 3 (-3x) y le añadimos 1 (+x). 6x - 3x + x = 4x.

En el miembro de la derecha nos queda 12 (4 + 8 = 12).

3º Nuestro objetivo final es tener x = algo.

Se pueden dar tres casos llegados a este punto:

- Que tengamos x = algo: ya estaría resuelta (ejemplo: x = 5).

- Que la x sea negativa: tenemos que cambiar el signo de la "x" y del resultado al otro lado (ejemplo:  -x = 7 pasaría a x = -7, cambiamos el signo de la "x" de negativo a positivo y el del 7 de positivo a negativo y ya estaría resuelta).

- Que haya un número (coeficiente) delante de la "x": en este caso pasamos ese número, incluyendo su signo sin cambiarlo, a dividir al resultado al otro lado. Lo calculamos y listo. Este es el caso del ejemplo con el que hemos empezado, y volviendo a él:

4x = 12

x = 12 : 4

x = 3

Recordad al hacer la última división que hay que aplicar las reglas de los signos en división:

+ : + = +

 - : - = +

+ : - = +

- : + = -

 

Además, algo interesante de las ecuaciones es que, una vez resueltas, podemos comprobar por nosotras mismas si el resultado es el correcto. ¿Cómo? Cambiando en la ecuación original, la que hemos empezado a resolver, las incógnitas por el valor que nos ha dado como resultado. En el ejemplo que hemos hecho sería cambiar las "x" por 3, lo que quedaría así:

6x - 8 = 3x + 4 - x

6·3 - 8 = 3·3 + 4 - 3

Hacemos las operaciones a cada lado y comprobamos si nos da el mismo resultado:

18 - 8 = 9 + 4 - 3

10 = 10

Si nos da lo mismo, se cumple la igualdad y el resultado es correcto. De no serlo... ¡mala suerte!. Hay que volver a empezar poniendo atención en no equivocarnos de nuevo.

 

Con esto terminamos las explicaciones de ecuaciones. La semana que viene (última ya del curso, al menos para matemáticas) veremos algo de longitudes, áreas y el teorema de Pitágoras. ¡Buen fin de semana!

PROPORCIONALIDAD INVERSA

Llegamos a la recta final del curso y, en este último tema, vamos a juntar contenidos diferentes que nos serán útiles en nuestro día a día. Para empezar, ayer estuvimos hablando de la proporcionalidad inversa.

Ésta consiste en una relación entre dos magnitudes (sean las que sean, como número de personas y dinero que cobran de un premio o velocidad de un vehículo y tiempo que tardamos en llegar a un sitio) en la que, al aumentar una de ellas disminuye la otra y viceversa.

Por ejemplo: 6 personas realizan un trabajo en 4 días. ¿Cuánto tardarían en hacer ese mismo trabajo 8 personas?

Lo primero que hacemos es localizar las magnitudes, en este caso número de personas y días. Después nos paramos a pensar... "si el mismo trabajo lo realizan más personas, ¿tardarán más o menos días?". La respuesta es sencilla y de lógica: si más personas hacen el mismo trabajo, tardarán menos tiempo. Por lo tanto, vemos que cuando una aumenta (número de personas) la otra disminuye (días que emplean). Así pues, se da una relación inversa.

                   PERSONAS                                       DÍAS

                      6-----------------------------------------------4

                      8-----------------------------------------------x

Para resolver este tipo de proporcionalidad (o regla de 3 inversa) también tenemos que multiplicar dos de los números y dividir entre el otro, pero aquí lo haremos multiplicando los dos que están en la misma línea y los dividiremos entre el que está con la incógnita en la otra.

La solución, por lo tanto, es que 8 personas realizan ese trabajo en 3 días.

De esto no vamos a ver más de momento. Hoy pasamos a las temidas ecuaciones, que ya veréis no son para tanto y dominaréis sin problemas. Os dejo una imagen que ejemplifica lo de la proporcionalidad inversa. ¡Hasta ahora!

CORRECCIÓN DEL TRABAJO

Os pongo aquí la corrección de los ejercicios del trabajo que hemos hecho este tema. Recordad que mañana lunes tenemos el examen. ¡Buena suerte a todas!

EXPOSICIONES DE LAS RECETAS

El jueves pasado hicimos la exposición y entrega de los trabajos interdisciplinares de las recetas de cocina. Todos estuvieron muy bien hechos, interesantes y, por supuesto, ¡riquísimos!

Os pongo unas cuantas fotografías de algunos momentos en esta entrada del blog y las de las presentaciones. Si queréis ver el resto y las de las presentaciones, aquí tenéis el enlace a ellas.

ARROZ CON LECHE

Empezamos con el grupo de las dos Anas, Simo y Araceli, que hicieron este delicioso postre.

EMPANADA DE ATÚN:

Después siguieron Pilar y Laura con esta receta en la que, al parecer, son todas unas expertas y triunfan en cada cumpleaños.

TORTILLA DE PATATA:

El grupo de Patricia, Maryla y Aisha (o "Kawai", como les gusta hacerse llamar) nos presentó este clásico reinterpretado a la "gambiana".

TARTA DE QUESO:

Por último Ximena, Gema y Juani nos trajeron esta riquísima receta, que se aleja de la típica con base de galleta y cobertura de mermelada pero a la que no tiene nada que envidiarle.

Ya solo nos faltaba probarlo todo, y fue lo que hicimos junto a unos refrescos y pan que habíais comprado para acompañar. En definitiva: una actividad distinta y que resultó la mar de rica. ¡Felicidades!